- 9. 카이제곱 검정 : 독립성 검정 (교차 분석) 목차

카이제곱의 마지막 검정 방법인 독립성 검정이다. 두 범주형 변수가 있을 때 서로 연관성이 있는 지, 혹은 독립인지 검정하는 방법이다. 예를 들자면, 연령때에 따른 자동차 선호도가 유의미 한가를 판단할 때 사용한다.
1. 카이제곱 독립성 검정 예제.
테이블 1: 영화 간식류 데이터에 대한 분할표
| 영화 장르 | 간식류 | 간식류 비구매 |
| 작업 | 50 | 75 |
| 코미디 | 125 | 175 |
| 가족 | 90 | 30 |
| 공포 | 45 | 10 |
다음 예제를 통해 카이제곱 독립성 검정을 알아보자.
2. 기대 개수 계산
각 영화-간식류 조합에 대한 기대 개수를 구하려면 먼저 아래 나온 행과 열 합계가 필요합니다.
테이블 2: 행 합계와 열 합계가 포함된 영화 간식류 데이터에 대한 분할표
(카이제곱 독립성 검정 예제 | 통계 소개 | JMP 를 참고하였습니다.)
| 영화 장르 | 간식류 | 간식류 비구매 | 행 총계 |
| 작업 | 50 | 75 | 125 |
| 코미디 | 125 | 175 | 300 |
| 가족 | 90 | 30 | 120 |
| 공포 | 45 | 10 | 55 |
| 열 총계 | 310 | 290 | 전체 합계 = 600 |
여기서 각 칸에 대한 기대 개수는 행*열/전체 로 구하면 된다.
식을 대입해서 각각을 계산하면 다음과 같이 나온다.
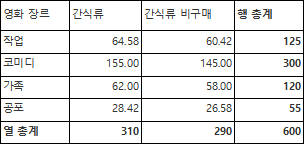
대략 반올림 하여 다음처럼 정리하였다.
| 영화 장르 | 간식류 | 간식류 비구매 | 행 총계 |
| 작업 | 50 65 |
75 60 |
125 |
| 코미디 | 125 155 |
175 145 |
300 |
| 가족 | 90 62 |
30 58 |
120 |
| 공포 | 45 28 |
10 27 |
55 |
| 열 총계 | 310 | 290 | 전체 합계 = 600 |
3. 검정 통계량 계산
검정 통계량을 구할 때는 (기대값-실제값)^2 / 기대값 이라는 공식으로 구해 줄 수 있다. (카이제곱 검정 통계량 공식)
이렇게 적용해서 값을 구하면 다음과 같이 값이 나온 다는 것을 알 수 있다.
| 영화 장르 | 간식류 | 간식류 비구매 |
| 작업 | 실제값: 50 기대값: 64.58 |
실제값: 75 기대값: 60.42 |
| 차이: 50 – 64.58 = -14.58 차이 제곱값: 212.67 기대값으로 나누기: 212.67/64.58 = 3.29 |
차이: 75 – 60.42 = 14.58 차이 제곱값: 212.67 기대값으로 나누기: 212.67/60.42 = 3.52 |
|
| 코미디 | 실제값: 125 기대값: 155 |
실제값: 175 기대값: 145 |
| 차이: 125 – 155 = -30 차이 제곱값: 900 기대값으로 나누기: 900/155 = 5.81 |
차이: 175 – 145 = 30 차이 제곱값: 900 기대값으로 나누기: 900/145 = 6.21 |
|
| 가족 | 실제값: 90 기대값: 62 |
실제값: 30 기대값: 58 |
| 차: 90 – 62 = 28 차이 제곱값: 784 기대값으로 나누기: 784/62 = 12.65 |
차이: 30 – 58 = -28 차이 제곱값: 784 기대값으로 나누기: 784/58 = 13.52 |
|
| 공포 | 실제값: 45 기대값: 28.42 |
실제값: 10 기대값: 26.58 |
| 차이: 45 – 28.42 = 16.58 차이 제곱값: 275.01 기대값으로 나누기: 275.01/28.42 = 9.68 |
차이: 10 – 26.58 = -16.58 차이 제곱값: 275.01 기대값으로 나누기: 275.01/26.58 = 10.35 |
이제 여기서 전체 검정 통계량을 구해준 다음 유의수준 내에서의 검정통계량과 비교하여 기각 여부를 판단하면 된다.
검정 통계량 합은 65.03이 나온 다는 사실을 우리는 쉽게 확인할 수 있다.
카이제곱, 독립성 검정에서의 자유도는 행,열 두가지에 의해 영향을 받는다.
자유도 공식은 다음과 같다. df=(r−1)×(c−1) 여기서는 행,열이 4,2 이므로 자유도는 3이 나온다.
4. 기각 여부 판단
카이제곱 그래프에서, 자유도가 3이고, 유의 수준이 0.05인 카이제곱 값은 7.815이다.
이는 우리가 구한 값인 65.03보다 작은 값이다. 즉 우리가 구한 카이제곱 검정 통계량은, 기각역에 속한다.
따라서 우리는 영화 장르와 간식류 구매는 서로 독립적이라는 가정을 기각할 수 있다.
즉, 영화 장르와 간식류 구매는 서로 연관성이 존재한다.
'Statistics > 통계 검정' 카테고리의 다른 글
| 8. 카이제곱 검정 2 : 동일성 검정 예제 (0) | 2021.07.07 |
|---|---|
| 7. 카이제곱 검정 : 적합도 검정 (Pearson의 카이제곱 검정) Goodness of fit test 예제. (1) | 2021.07.06 |
| 6. 통계 검정 기초 : Wilcoxon Rank sum 검정/Mann Whitney U 검정 예제, 정규분포가 아닐때 (0) | 2021.07.05 |
| 5. 통계 검정 기초 : Wilconxon Signed Rank검정(윌콕슨 부호 순위 검정) 예제, 정규분포가 아닐때 (1) | 2021.07.04 |
| 4. 통계 검정 기초 , 독립 표본 T검정 : 이분산일때 (Welch`s t test) (0) | 2021.07.02 |




