5. 통계 검정 기초 : Wilconxon Signed Rank검정(윌콕슨 부호 순위 검정) 예제, 정규분포가 아닐때

1. Wilcoxon 검정이란?

 

만약 모집단이 정규성을 만족하지 않는 다면 어떻게 해야할까? 정규성이 만족하지 않는 경우에는 T검정 Z검정등 우리가 기존에 공부한 검정 방법을 적용할 수 없다. 왜냐하면 이 검정 방법들의 사전 가정은 모집단이 정규 분포를 만족한다는 전제가 깔려 있기 때문이다. 

 

하지만 우리의 실제 생활에서 분석되는 통계 자료들은 정규성을 만족하지 않는 경우가 많다. 이럴 때는 어떤 방식으로 통계 검정을 해야하는 가 오늘 알아보자. 

 

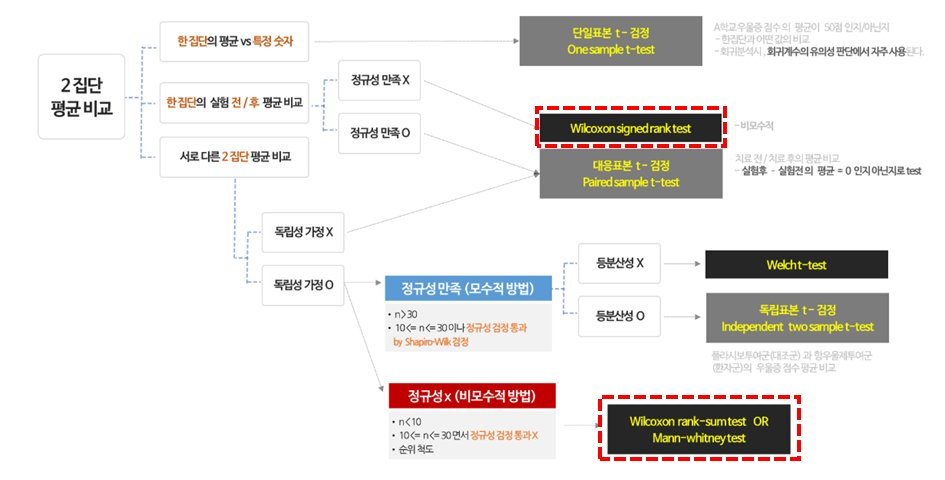
다음 그림은 데이터 자료에 붙여둔 통계 검정 정리표이다. 오늘 공부할 내용은, Wilcoxon 이며, 이게 어떤 분석인지 한 눈에 파악하기 쉽도록 표를 붙여 놓았다. 

 

※ 그림 출처 https://nittaku.tistory.com/467

 

 

---

2. Wilcoxon 검정의 종류

 

Wilcoxon 검정이란 모집단이 정규성을 만족하지 못할 때 사용하는 검정으로, 두 모집단의 관계에 따라 2종류로 나뉜다. 

두 모집단이 서로 연관성을 가진다면, Wilcoxon signed rank test (윌콕슨 부호 순위 검정)를 두 모집단이 서로 독립이라면, wilcoxon rank sumtest 혹은 Mann - Whitney test 검정 방법을 사용한다. 

 

 

2-1. Wilcoxon signed rank test (윌콕슨부호순위검정)

 

이 TEST는 T 검정과 같이 목적은 두 그룹의 평균이 같은지 여부를 비교하는 비모수적 분석 방법이다. 

정규분포를 따르지 않거나(표본의 크기가 10이하로 작거나) 분포 형태를 모를 경우의 중위값 차이에 의한 비모수 검정이라고 생각하면 된다. 

 

두 모집단의 관계는 연관되어 있고, 이 모집단에서 랜덤하게 표본을 구하면 다음과 같이 나온다. 

 

• (X1,Y1),(X2,Y2),...,(Xn,Yn)(X1,Y1),(X2,Y2),...,(Xn,Yn)X1−Y1,X2−Y2,...,Xn−Yn∼F(x−Δ)X1−Y1,X2−Y2,...,Xn−Yn∼F(x−Δ)

 

귀무가설은 위치 모수가 0이다 라고 가정한다. 자연스럽게 대립가설은 위치모수가 0이 아니다가 된다. 

 

• H0:Δ=0 v.s. H1:Δ≠0

 

두 표본의 절대차 |Yi−Xi|=0|Yi−Xi|=0을 제외한 절대차의 순위(rank)라고 하면 검정 통계량 W 는 다음과 같다.

 

5 장 가설검정 의학통계 (dongguk.ac.kr)

 

 

 

---

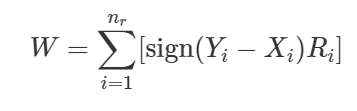
2-2. Wilcoxon signed rank test (윌콕슨부호순위검정) 예시

 

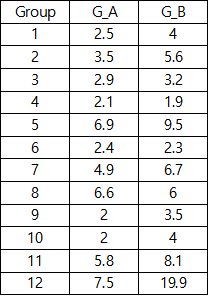
다음과 같이 치료제 투약 전의 약 효과에 따른 관측 값이 A _ B 로 관측되었다고 하자. 

모수가 적으며, 정규 분포를 따르지 않을 때, 검증 방법으로 치료제 투약이 효과가 있는 지 검정할 것이다. 

 

 

 

1. 귀무가설 세우기. 

 

윌콕슨 부호,순위 검정에서의 귀무가설은 중위값이 0이다. 

 

• H0:Δ=0 v.s. H1:Δ≠0

 

2. 두 그룹간 차이 구하기. 

 

윌콕슨에서의 핵심은 두 그룹간의 차이를 구한 뒤, 그 차이의 값을 절대값으로 순위를 매겨 부호별로 판단하는 방법이다.  이를 위해서, 두 그룹간 차이를 구한 뒤, 절대값을 씌워 순위를 구해보았다. 

 

참고로 그룹간 차이를 구할 때에는 약 투약 후 Group - 약 투약 전 Group 즉, G_B - G_A 이다. 

 

• 차이 : (G_B) - (G_A)

 

 

 

그러면 다음과 같이 정리할 수 있다. 이를 조금 더 보기 좋게 정리하면 다음과 같다. 

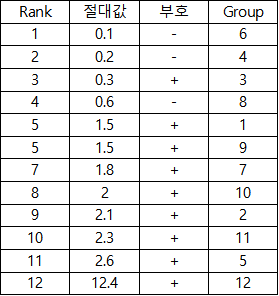
이는 각 Rank 별로 절대값과 부호 그리고 Group 순위를 순서대로 나열한 값이다. 

 

 

3. Wilcoxon 부호 순위 검정 

 

여기서 Wilcoxon 부호 순위 검정 방법은 다음과 같이 적용 가능하다. 

 

먼저, 순위 절대값이 - 인 Group ,+ 인 Group을 따로 분리하여야 한다. 

 

[ '-' 부호 Group ]

• 이 그룹의 Rank 값을 더해주어야 한다. 
• 즉, 1+2+4 = 7 이 나온다. 

[ '+' 부호 Group ]

 

• 이 그룹의 Rank 값을 더해주어야 한다. 
• 3+5.5+5.5+7+8+9+10+11+12 = 71

*주의 할 점은, 5/6 Rank 의 값이 같으므로 5->5.5, 6->5.5 가 들어가야 한다. 

 

 

4. 귀무가설 기각 여부 판단하기 

 

W- 값이 7이고, W+값이 71이다. 여기서 윌콕슨 검정은 작은 값을 채택한다. 

따라서 W 값을 7로 채택한다. 

 

양측 검정 TEST를 시작한다면 윌콕스 Rank TEST 에서 P-Value 0.05 수준에서 검증한다는 가정하에, 

13이라는 값이 나옴을 알 수 있다. (아래 표 참고)

 

 

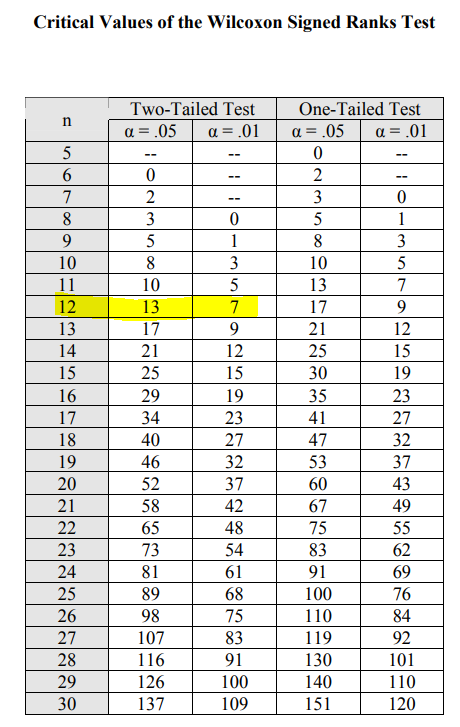
즉, 우리가 구한값 Wsiai=7, 윌콕슨 값 W=erit=13 이 되고, 

Wsiai < Werit (7<13) 이 되므로, 귀무가설은 기각된다.  즉, 투약 약이 효과가 있다고 판단할 수 있다. 

 

 

5. 만약 n(n+1)/2 가 20 보다 크다면 Z검정을 통해 판단할 수 있다. 

 

 

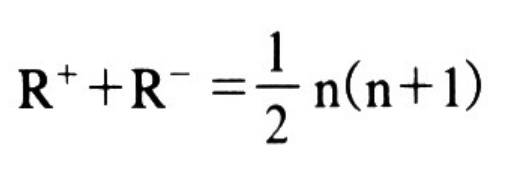
윌콕슨 검정 값은 다음과 같은 식이 성립된다.  (R+ =W+ 이며, R- 는 W- 임.)

현재 예시는 n=12이므로 (W+ + W- =78) = 12*13/2 =78 이 나온다. 

 

검정통계량 중 작은 값 즉, W-를 T라고 하는데, 데이터가 모두 같은 방향으로 변화한다면, T=0이 되고, 변화의 방향이 일정하지 않는 다면 T 값은 커지게 된다. 커진 T 값은 n(n+1)/4,이 된다. 

 

T 값은 근사적으로 평균이 n(n+1)/4, 표준편차가 √((n(n+1)(2n+1))/24) 인 정규 분포를 따르게 된다. 

 

 

 

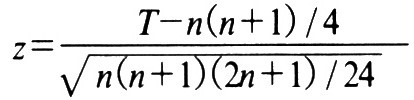
여기서 추가적으로 tied ranks 라고 현재 5,6번이 동일한 순위(t=2)를 가졌기 때문에 σ 값에서 t^3-t/48 을 빼주어야 한다. 여기에서는 t=2 이므로 8-2/48=0.125 가 나온다. 그래서 다음 식에서 0.125를 반영한 값까지 계산하면 아래와 같다. 

 

 

• μ: n(n+1)/4.
• σ: √((n(n+1)(2n+1))/24)

즉 Z값은 다음과 같이 구해진다. 

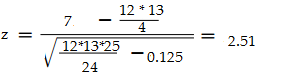
Z값을 P-Value로 변환하면 Excel =1-ERF(ABS(2.51)/SQRT(2)) , 0.012임을 확인할 수 있다. 

 

양측 검정에서 0.05 신뢰 수준에 대한 기각역은  Z>1.96, Z<-1.96 이고, Z값은 기각역에 속해 있으므로, 귀무가설이 기각된다. 따라서 치료 약은 효과가 있다 라고 판단할 수 있다.