- 7. 카이제곱 검정 : 적합도 검정 (Pearson의 카이제곱 검정) Goodness of fit test 예제. 목차

1. 카이제곱 검정
카이 제곱 검정은, 관찰된 빈도가 기대되는 빈도와 유의미하게 다른지를 검증하는 통계 검정 방법이다.
주로 범주형 자료로 구성된 데이터 분석에 이용된다. 핵심은 두 범주형 변수가 서로 상관이 있는 지 혹은 독립 관계인지 이다. 참고로 범주형 자료는 categorical data 로, 월 소득 100만원 미만, 이상 등 구간에 대한 자료를 의미한다.
카이제곱 검정의 형태는 다음과 같다.
1. Goodness of fit test : 적합도 검정. (Pearson의 카이제곱 검정)
적합도 검정이란, 어떤 모집단의 표본이 그 모집단을 대표할 수 있는 지 검정하는 방법으로, 관찰 된 비율 값이 기대값과 같은지 여부를 검정하는 방법이다. 변수는 1개 이다.
2. Test of homogeneity : 동질성 검정.
동질성 검정이란, 두 집단의 분포가 동일한지 검정하는 방법이다.
3. Test for independence : 독립성 검정.
동립성 검정은 두 개 이상의 변수가 독립인지 검정하는 방법이다. 즉, 각 표본들이 관찰 값에 영향을 주는지 여부를 검정하는 방법이다.

2. 적합도 검정. (Pearson의 카이제곱 검정)
간단한 예시를 통해서 적합도 검정에 대해 알아보자. 참고한 홈페이지는 statistics Knowledge 포털을 참고했다.
2.1 적합도 검정 조건
- 범주형 변수 값의 갯수를 알 때 (단순 랜덤 표본에 해당하는 값이어야 함)
- 범주형, 명목형, 연속형 데이터에는 적합하지 않음.
- 관측된 각 데이터 범주에서 최소 5개의 값이 기대될 정도의 사이즈.
2.2 적합도 검정 예제.
랜던 표본으로 10개의 사탕을 수집했다. 각 봉지에 5가지 맛과 100개의 사탕이 들어있다.
가설은 봉지마다 담긴 다섯 가지 맛의 비율이 동일하다.
2.2.1 적합도 검정 조건 Check
- 범주형 변수 값의 갯수를 알 때 (단순 랜덤 표본에 해당하는 값이어야 함) -> 캔디는 10봉지이다.
- 범주형, 명목형, 연속형 데이터에는 적합하지 않음. -> 범주형 변수 = 캔디의 맛. 맛별 개수는 5가지.
- 관측된 각 데이터 범주에서 최소 5개의 값이 기대될 정도의 사이즈. => 맛 별 캔디수는 200으로 5보다 큼.
실제 값은 다음과 같이 나왔다고 가정하자.
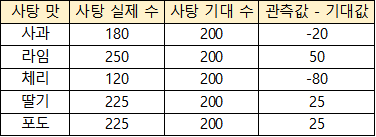
2.2.2 카이제곱 검정 값 구하기.

다음 위 식을 사용하여 카이제곱 검정 값을 구해주자.
위 식에서 우리는 관측값 - 기대값의 제곱값을 기대값으로 나누고 모두 더해 준 값이 카이제곱 검정 값임을 확인할 수 있다. 즉 하나하나 구해보면 하기 식의 값과 같다.
차이제곱 / 기대값의 총 합이 카이제곱 검정값이 되므로,
카이제곱 검정 값 = 2 + 12.5 + 32 + 3.125 + 3.125 = 52.75 이다.

2.2.3 카이제곱 검정 판단 하기.
신뢰수준을 5%라고 하면 유의 수준은 0.05가 나온다.
검정 통계량은 52.75이고, 자유도는 5-1=4 가 나온다.
0.05 유의수준 에서의 자유도 4인 카이제곱값은 9.488이므로, 우리가 구한 값이 더 크다.
즉, 귀무가설을 기각 할 수 있다.
52.75 > 9.488
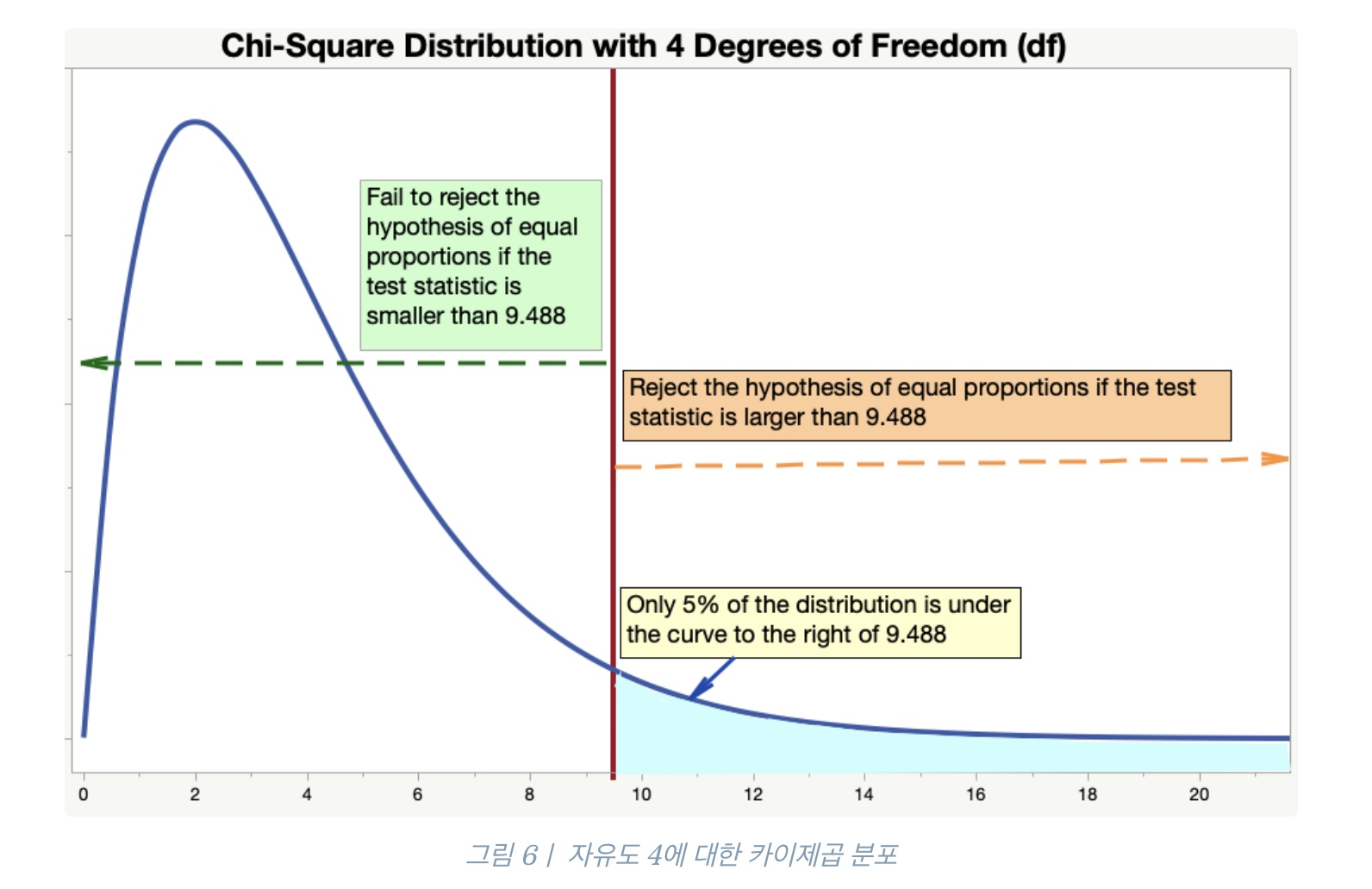
그래프를 이용해서 이해해 보자면, 다음 그림이 바로 자유도가 4일 때의 카이제곱 그래프이다.
우리가 정한 유의수준 0.05, 자유도 4에서의 카이제곱 함수는 9.488이며 이는 오직 5%의 데이터만이 오른쪽 꼬리 영역에 속하는 데이터임을 확인할 수 있다. 우리가 구한 검정 통계량은 무려 52.75 이므로 이는 임계값보다는 극단값에 훨씬 가깝다는 사실을 확인할 수 있다.
그림에서 파란 색 부분이 기각역 영역이라고 생각하면 된다. 따라서 각 봉지마다 담긴 캔디 수는 동일하지 않다.
보통 P 값으로 소프트웨어에서 검정 결과가 나오는 데, 이 데이터를 이용해서 보면, P-값은 P < 0.0001이 나오게 된다. 이를 다시 해석하면, 귀무가설이 맞다고 가정할 때 다른 10봉지 표본에서 검정 통계량보다 더 극단값을 보일 확률은 10000분의 1보다 낮다는 의미로 해석할 수 있다. 즉 귀무가설은 기각된다.
'Statistics > 통계 검정' 카테고리의 다른 글
| 9. 카이제곱 검정 : 독립성 검정 (교차 분석) (0) | 2021.07.08 |
|---|---|
| 8. 카이제곱 검정 2 : 동일성 검정 예제 (0) | 2021.07.07 |
| 6. 통계 검정 기초 : Wilcoxon Rank sum 검정/Mann Whitney U 검정 예제, 정규분포가 아닐때 (0) | 2021.07.05 |
| 5. 통계 검정 기초 : Wilconxon Signed Rank검정(윌콕슨 부호 순위 검정) 예제, 정규분포가 아닐때 (1) | 2021.07.04 |
| 4. 통계 검정 기초 , 독립 표본 T검정 : 이분산일때 (Welch`s t test) (0) | 2021.07.02 |



