- 6. 통계 검정 기초 : Wilcoxon Rank sum 검정/Mann Whitney U 검정 예제, 정규분포가 아닐때 목차
- 1. Wilcoxon Rank sum TEST (Mann Whitney U) 란?
- 2. Wilcoxon Rank sum TEST (Mann Whitney U) 예제

이번에는 두 모집단이 독립이면서 정규분포를 따르지 않을 때의 검정 방법이다.
Wilcoxon Rand sum TEST (윌콕슨 순위 합 검정) 혹은 Mann Whitney U 검정이라고 불린다.
1. Wilcoxon Rank sum TEST (Mann Whitney U) 란?
Mann Whitney U 검정이라고도 잘 알려져 있는 이 검정은, 표본이 서로 독립일때의 비모수 검정 방법이다. 두 모집단의 표본의 갯수가 다를 때 사용 가능하다. 이 검정은 임의로 선택된 X값과 Y 값에 대해서 X가 Y보다 클 확률과 Y가 X보다 클 확률이 같다고 귀무가설을 세운다. 즉, X와 Y의 데이터가 중앙값이 같은 연속된 분포에서 추출된 표본이다 라고 할 수 있다. 이 말은 두 모집단의 중앙값이 동일한지 여부를 검정한다는 의미이다.
2. Wilcoxon Rank sum TEST (Mann Whitney U) 예제

유의수준 5%에서 다음을 검증하라 라는 문제가 주어졌다고 하자.
1. 귀무가설 세우기.
귀무가설은 다음과 같다. Group A와 B에서의 값은 같은 중앙값이 같은 연속된 분포에서 추출된 표본값을 가진다.
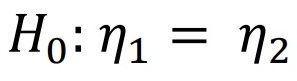
2. 각 데이터 순위 결정하기.
순위를 쉽게 정하기 위해 다음과 같이 데이터를 정리한 뒤, 순위를 정해준다.
엑셀을 이용해서 구했고, RANK.AVG 를 사용하면, 같은 값에 대해 평균 값으로 값을 반환해준다.
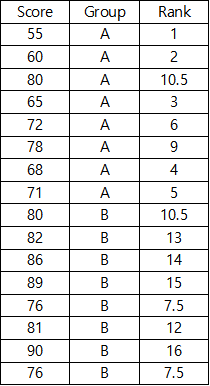
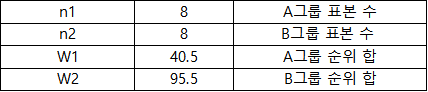
3. 각각의 값을 구해준다.
여기서 Ua,b = Ranksum - n(n+1)/2 이므로, 각각의 Ua와 Ub의 값은 다음과 같다.
- Ua = 40.5 - 8*9/2 = 4.5
- Ub= 95.5 - 8*9/2 = 59.5
U의 최소값은 4.5가 됨을 확인할 수 있다.
아래의 Mann-Whitney U 검정 표에 따르면 n1,n2가 8,8이며, 유의수준 0.05에서의 값이 13임을 확인 할 수 있다.
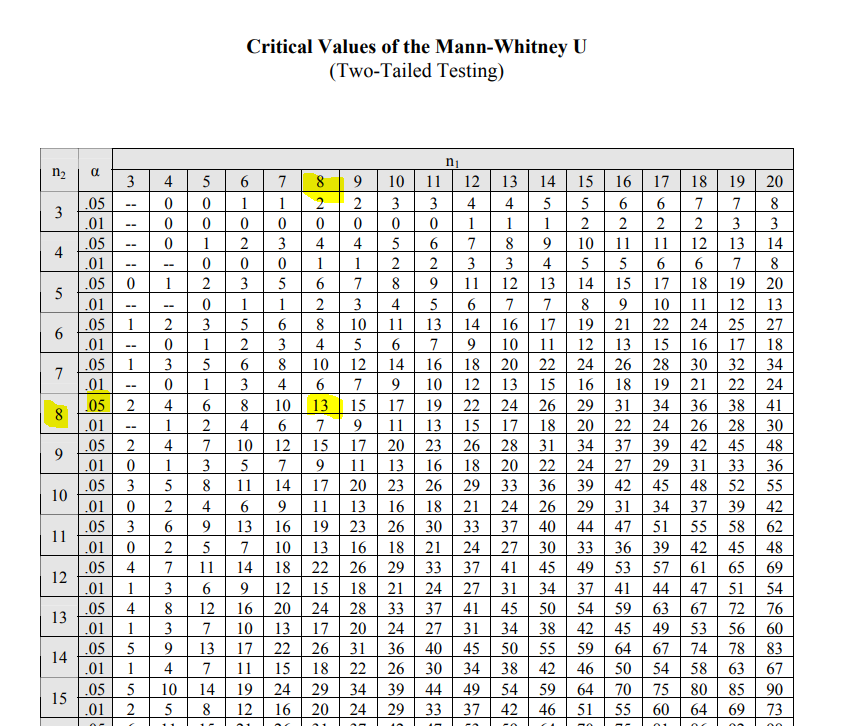
4. 귀무가설 기각 여부 판단하기
우리가 구한값 4.5는 맨-휘트니 표의 13보다 작은 값 이다. 따라서 귀무가설이 기각된다.
즉 Group A,B에는 차이점이 존재한다.
5. Z 검정을 통해 확인하기.
이번에도 역시 Z 검정을 이용해서 검정해보자. 각각의 U값은 표본 수와 총합을 이용해서 구할 수 있다. (R1은 Groua A의 Rank 총 합이다. )
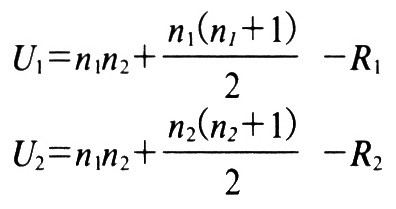
즉 위의 식을 이용해서 계산하면,
U1 = 8*8 +8*9/2 -40.5 = 59.5
U2 = 8*8 +8*9/2 -95.5 = 4.5
(사실 이 값은 Ua,b = Ranksum - n(n+1)/2 와 같다 )
- Umin 값 = 4.5
- 평균 값 = (U1+U2)/2 =32
- 표준 편차 = 루트(n1*n2*(n1+n2+1)/12) = 9.52
각각의 값을 구했으므로 Z 값을 구해준다.
Z 값은 아래의 식과 같다 (Z=(Umin-평균) / 표준편차))
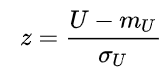
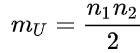
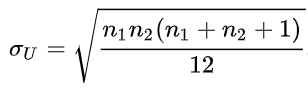
Standardized Value
따라서 Z = (4.5-32)/9.52 = - 2.889 라는 값이 나온다.
(Umax 로 계산해도 상관 없다. Umax로 계산하면 2.889가 나온다. )
사실 여기에서도 등수가 동일한 tied 표본이 있을 때는 Z 값을 보정해야 하지만, Z 값 보정하지 않아도 큰 차이가 없다.
만약 보정하고 싶다면, 표준편차를 보정값으로 다시 계산하면 된다. 보정값은 다음과 같다.
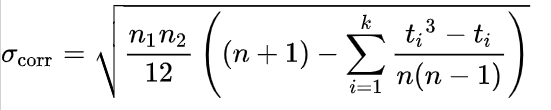
P-Value 0.05 수준에서 검증하면, Z score의 기각역은 >1.96, <-1.96 범위에 존재하게 된다. 우리가 구한 Z 값은 -2.889로 <-1.96 범위에 속하기 때문에 기각 영역에 속한다. 즉 귀무가설을 기각할 수 있다.
'Statistics > 통계 검정' 카테고리의 다른 글
| 8. 카이제곱 검정 2 : 동일성 검정 예제 (0) | 2021.07.07 |
|---|---|
| 7. 카이제곱 검정 : 적합도 검정 (Pearson의 카이제곱 검정) Goodness of fit test 예제. (1) | 2021.07.06 |
| 5. 통계 검정 기초 : Wilconxon Signed Rank검정(윌콕슨 부호 순위 검정) 예제, 정규분포가 아닐때 (1) | 2021.07.04 |
| 4. 통계 검정 기초 , 독립 표본 T검정 : 이분산일때 (Welch`s t test) (0) | 2021.07.02 |
| 3. 통계 검증 기초 - 독립 표본 T 검정 (검정 방법/예시) : 등분산 가정일 때 (0) | 2021.06.30 |



