- 5. 통계 검정 기초 : Wilconxon Signed Rank검정(윌콕슨 부호 순위 검정) 예제, 정규분포가 아닐때 목차
- 1. Wilcoxon 검정이란?
- 2. Wilcoxon 검정의 종류

1. Wilcoxon 검정이란?
만약 모집단이 정규성을 만족하지 않는 다면 어떻게 해야할까? 정규성이 만족하지 않는 경우에는 T검정 Z검정등 우리가 기존에 공부한 검정 방법을 적용할 수 없다. 왜냐하면 이 검정 방법들의 사전 가정은 모집단이 정규 분포를 만족한다는 전제가 깔려 있기 때문이다.
하지만 우리의 실제 생활에서 분석되는 통계 자료들은 정규성을 만족하지 않는 경우가 많다. 이럴 때는 어떤 방식으로 통계 검정을 해야하는 가 오늘 알아보자.
다음 그림은 데이터 자료에 붙여둔 통계 검정 정리표이다. 오늘 공부할 내용은, Wilcoxon 이며, 이게 어떤 분석인지 한 눈에 파악하기 쉽도록 표를 붙여 놓았다.
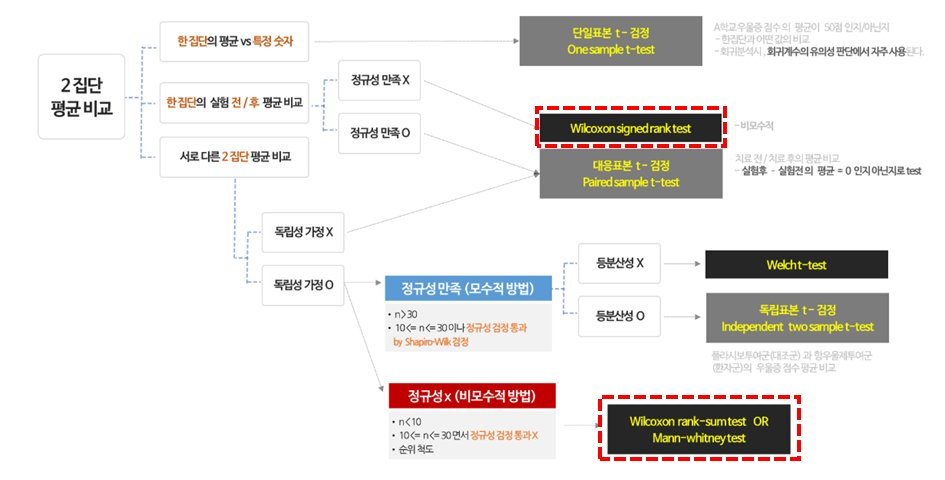
2. Wilcoxon 검정의 종류
Wilcoxon 검정이란 모집단이 정규성을 만족하지 못할 때 사용하는 검정으로, 두 모집단의 관계에 따라 2종류로 나뉜다.
두 모집단이 서로 연관성을 가진다면, Wilcoxon signed rank test (윌콕슨 부호 순위 검정)를 두 모집단이 서로 독립이라면, wilcoxon rank sumtest 혹은 Mann - Whitney test 검정 방법을 사용한다.
2-1. Wilcoxon signed rank test (윌콕슨부호순위검정)
이 TEST는 T 검정과 같이 목적은 두 그룹의 평균이 같은지 여부를 비교하는 비모수적 분석 방법이다.
정규분포를 따르지 않거나(표본의 크기가 10이하로 작거나) 분포 형태를 모를 경우의 중위값 차이에 의한 비모수 검정이라고 생각하면 된다.
두 모집단의 관계는 연관되어 있고, 이 모집단에서 랜덤하게 표본을 구하면 다음과 같이 나온다.
- (X1,Y1),(X2,Y2),...,(Xn,Yn)X1−Y1,X2−Y2,...,Xn−Yn∼F(x−Δ)
귀무가설은 위치 모수가 0이다 라고 가정한다. 자연스럽게 대립가설은 위치모수가 0이 아니다가 된다.
두 표본의 절대차 |Yi−Xi|=0을 제외한 절대차의 순위(rank)라고 하면 검정 통계량 W 는 다음과 같다.
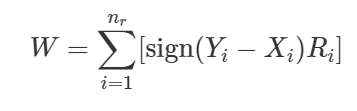
2-2. Wilcoxon signed rank test (윌콕슨부호순위검정) 예시
다음과 같이 치료제 투약 전의 약 효과에 따른 관측 값이 A _ B 로 관측되었다고 하자.
모수가 적으며, 정규 분포를 따르지 않을 때, 검증 방법으로 치료제 투약이 효과가 있는 지 검정할 것이다.
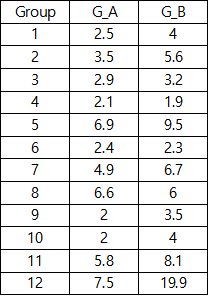
1. 귀무가설 세우기.
윌콕슨 부호,순위 검정에서의 귀무가설은 중위값이 0이다.

그러면 다음과 같이 정리할 수 있다. 이를 조금 더 보기 좋게 정리하면 다음과 같다.
이는 각 Rank 별로 절대값과 부호 그리고 Group 순위를 순서대로 나열한 값이다.
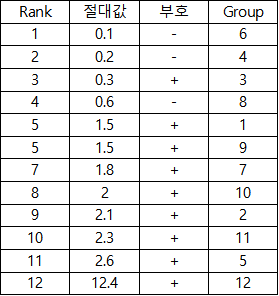
3. Wilcoxon 부호 순위 검정
여기서 Wilcoxon 부호 순위 검정 방법은 다음과 같이 적용 가능하다.
먼저, 순위 절대값이 - 인 Group ,+ 인 Group을 따로 분리하여야 한다.
[ '-' 부호 Group ]
- 이 그룹의 Rank 값을 더해주어야 한다.
- 즉, 1+2+4 = 7 이 나온다.
[ '+' 부호 Group ]
- 이 그룹의 Rank 값을 더해주어야 한다.
- 3+5.5+5.5+7+8+9+10+11+12 = 71
*주의 할 점은, 5/6 Rank 의 값이 같으므로 5->5.5, 6->5.5 가 들어가야 한다.
4. 귀무가설 기각 여부 판단하기
W- 값이 7이고, W+값이 71이다. 여기서 윌콕슨 검정은 작은 값을 채택한다.
따라서 W 값을 7로 채택한다.
양측 검정 TEST를 시작한다면 윌콕스 Rank TEST 에서 P-Value 0.05 수준에서 검증한다는 가정하에,
13이라는 값이 나옴을 알 수 있다. (아래 표 참고)
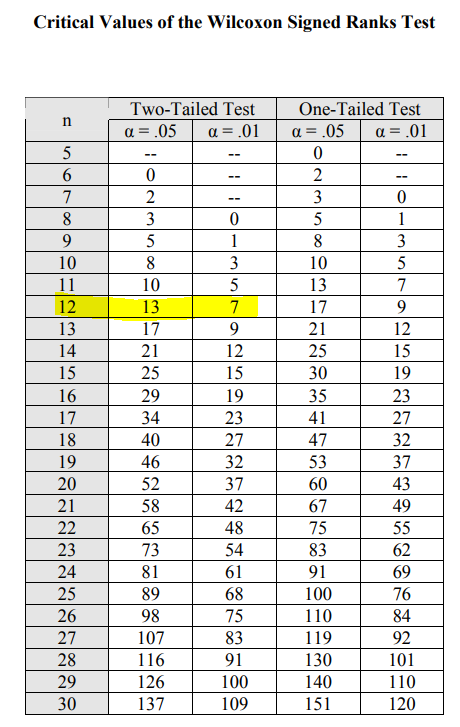
즉, 우리가 구한값 Wsiai=7, 윌콕슨 값 W=erit=13 이 되고,
Wsiai < Werit (7<13) 이 되므로, 귀무가설은 기각된다. 즉, 투약 약이 효과가 있다고 판단할 수 있다.
5. 만약 n(n+1)/2 가 20 보다 크다면 Z검정을 통해 판단할 수 있다.
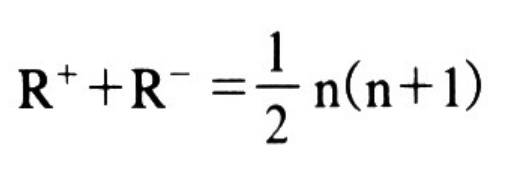
윌콕슨 검정 값은 다음과 같은 식이 성립된다. (R+ =W+ 이며, R- 는 W- 임.)
현재 예시는 n=12이므로 (W+ + W- =78) = 12*13/2 =78 이 나온다.
검정통계량 중 작은 값 즉, W-를 T라고 하는데, 데이터가 모두 같은 방향으로 변화한다면, T=0이 되고, 변화의 방향이 일정하지 않는 다면 T 값은 커지게 된다. 커진 T 값은 n(n+1)/4,이 된다.
T 값은 근사적으로 평균이 n(n+1)/4, 표준편차가 √((n(n+1)(2n+1))/24) 인 정규 분포를 따르게 된다.
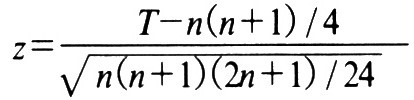
여기서 추가적으로 tied ranks 라고 현재 5,6번이 동일한 순위(t=2)를 가졌기 때문에 σ 값에서 t^3-t/48 을 빼주어야 한다. 여기에서는 t=2 이므로 8-2/48=0.125 가 나온다. 그래서 다음 식에서 0.125를 반영한 값까지 계산하면 아래와 같다.
- μ: n(n+1)/4.
- σ: √((n(n+1)(2n+1))/24)
즉 Z값은 다음과 같이 구해진다.
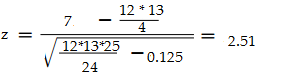
Z값을 P-Value로 변환하면 Excel =1-ERF(ABS(2.51)/SQRT(2)) , 0.012임을 확인할 수 있다.
양측 검정에서 0.05 신뢰 수준에 대한 기각역은 Z>1.96, Z<-1.96 이고, Z값은 기각역에 속해 있으므로, 귀무가설이 기각된다. 따라서 치료 약은 효과가 있다 라고 판단할 수 있다.
'Statistics > 통계 검정' 카테고리의 다른 글
| 7. 카이제곱 검정 : 적합도 검정 (Pearson의 카이제곱 검정) Goodness of fit test 예제. (1) | 2021.07.06 |
|---|---|
| 6. 통계 검정 기초 : Wilcoxon Rank sum 검정/Mann Whitney U 검정 예제, 정규분포가 아닐때 (0) | 2021.07.05 |
| 4. 통계 검정 기초 , 독립 표본 T검정 : 이분산일때 (Welch`s t test) (0) | 2021.07.02 |
| 3. 통계 검증 기초 - 독립 표본 T 검정 (검정 방법/예시) : 등분산 가정일 때 (0) | 2021.06.30 |
| 2. 통계 검증 기초 - 대응 표본 T 검정 (0) | 2021.06.29 |



